Determination of the Mueller matrix from intensity-based images recorded by a bright-field microscope

The hallmark of polarization-sensitive microscopy is the estimation of polarimetric information of samples, making them a suitable tool for detecting and diagnosis different type of cells and tissues in life sciences. In this work, we describe a practical procedure for measuring the Mueller matrix of samples using a bright-field microscope using 36 intensity-based images. The hallmark of the proposed method is the retrieval of the Mueller matrix across the transverse section of a sample, being suitable for analyzing biological samples. The method has been implemented in Python and MATLAB.

Mueller matrix and retrieval of polarization properties

Polarization-sensitive microscopy is a technique that allows obtaining the polarization properties of biological and material samples. Over the last decade, polarization-sensitive microscopy has been widely used in biological studies since it enables detecting states and diseases in biological samples analyzing their polarimetric properties. Polarization-based techniques are commonly based on estimating the Jones or Mueller matrices. Whereas the estimation of the Jones matrix requires an optical interferometer, the Mueller matrix can be estimated directly from intensity-based images, resulting in a more simple optical configuration. Another advantage of Mueller formalism is its applicability to polarized and depolarized light. Therefore, using Mueller formalism, one can recover the birefringence, diattenuation, and depolarization in a single measurement. Since these three parameters represent the polarization properties of a biological sample completely, the Mueller approach results in a powerful tool for biological samples.

Method to estimate the Mueller matrix

Here, we propose a computational method to estimate the Mueller matrix for a complex sample whose polarimetric properties vary across its transverse field of view. The method requires 36 images that are recorded by changing the polarization state of both, the polarization state generator (PSG) and polarization state analyzer (PSA) systems. Based on these polarization states of PSG and PSA systems, the Mueller matrix, M¸ is

$M=\begin{bmatrix}m_{00}&m_{01}&m_{02}&m_{03}\\m_{10}&m_{11}&m_{12}&m_{13}\\m_{20}&m_{21}&m_{22}&m_{23}\\m_{30}&m_{31}&m_{32}&m_{33} \end{bmatrix}$

where each element of the Mueller matrix is estimated by adding and/or subtracting 4 of the 36 images

$\begin{matrix}m_{00}=HH{+}HV{+}VH{+}VV&m_{01}=HH{+}HV{-}VH{-}VV\\m_{02}=PH{+}PV{-}MH{-}MV&m_{03}=RH{+}RV{-}LH{-}LV\\m_{10}=HH{-}HV{+}VH{-}VV&m_{11}=HH{-}HV{-}VH{+}VV\\m_{12}=PH{-}PV{-}MH{+}MV&m_{13}=RH{-}RV{-}LH{+}LV\\m_{20}=HP{-}HM{+}VP{-}VM&m_{21}=HP{-}HM{-}VP{+}VM\\m_{22}=PP{-}PM{-}MP{+}MM&m_{23}=RP{-}RM{-}LP{+}LM\\m_{30}=HR{-}HL{+}VR{-}VL&m_{31}=HR{-}HL{-}VR{+}VL\\m_{32}=PR{-}PL{-}MR{+}ML&m_{33}=LL{-}RL{-}LR{+}RR\\\end{matrix}$

In the last equation, the first letter represents the polarization state of the PSG system, and the second one corresponds to the polarization state of the PSA system. For example, based on this notation, in the HV image, the polarization state of the PSG and PSA systems are horizontal and vertical, respectively. Once the Mueller matrix is calculated, we can estimate the values of the diattenuation (D), polarizance (P), depolarization (Δ), and the angle of polarization (θ) via the following equations

$D=\frac{\sqrt{m_{01}^2+m_{02}^2+m_{03}^2}}{m_{00}}$

$P=\frac{\sqrt{m_{10}^2+m_{20}^2+m_{30}^2}}{m_{00}}$

$\Delta=1-\frac{\sqrt{\left(\sum_{i=0}^{3}m_{ii}^2\right)-m_{00}^2}}{\sqrt3m_{00}}$

$\theta=\frac{1}{2}{tan}^{-1}{\left(\frac{\sqrt{m_{20}^2+m_{30}^2}}{m_{10}}\right)}$

The polarization angle θ is only relevant if the optical element is a linear polarizer.

Experimental Results

We have reconstructed the polarimetric information of a linear polarizer (LPVISE100-A, Thorlabs) oriented at two angles: 90 degrees and +45 degrees. The linear polarizer in the experimental bright-field microscope is illuminated by a beam of light emerging of a collimated laser-diode-pumped DPSS laser (CPS532, Thorlabs source). The microscope is composed of an infinity-corrected MO with a lateral magnification of 40× and numerical aperture of NA = 0.75 and an tube lens of 200-mm focal length. A Basler acA5472-17um CMOS sensor (5472×3648 pixels, 2.4-µm square pixel size) is placed at the microscope’s image plane, allowing the acquisition of the intensity-based images.

To provide polarization-sensitive measurements, we insert the PSG and PSA systems in the microscope. The elliptical polarization state of the illumination source was changed to randomly polarized using a quartz depolarizer (DPU-25-A, Thorlabs). Thus, the polarizing elements of the PSG and PSA systems are two linear polarizers (LPVISE100-A, Thorlabs) and two achromatic quarter wave-plates (AQWP10M-580, Thorlabs). See the next figure.

Experimental Setup

From the recorded 36 intensity-based images, we have estimated their corresponding Mueller matrices. Comparison between the theoretical and experimental values for the Mueller matrix of the LP at the two angular position is shown in the next figure. For both orientation angles, we have estimated the mean and the standard deviation value of each element of the Mueller matrix (values also reported in the figure).

Matrix at 90 deg theoretical and experiemntal

Matrix at 45 deg theoretical and experiemntal

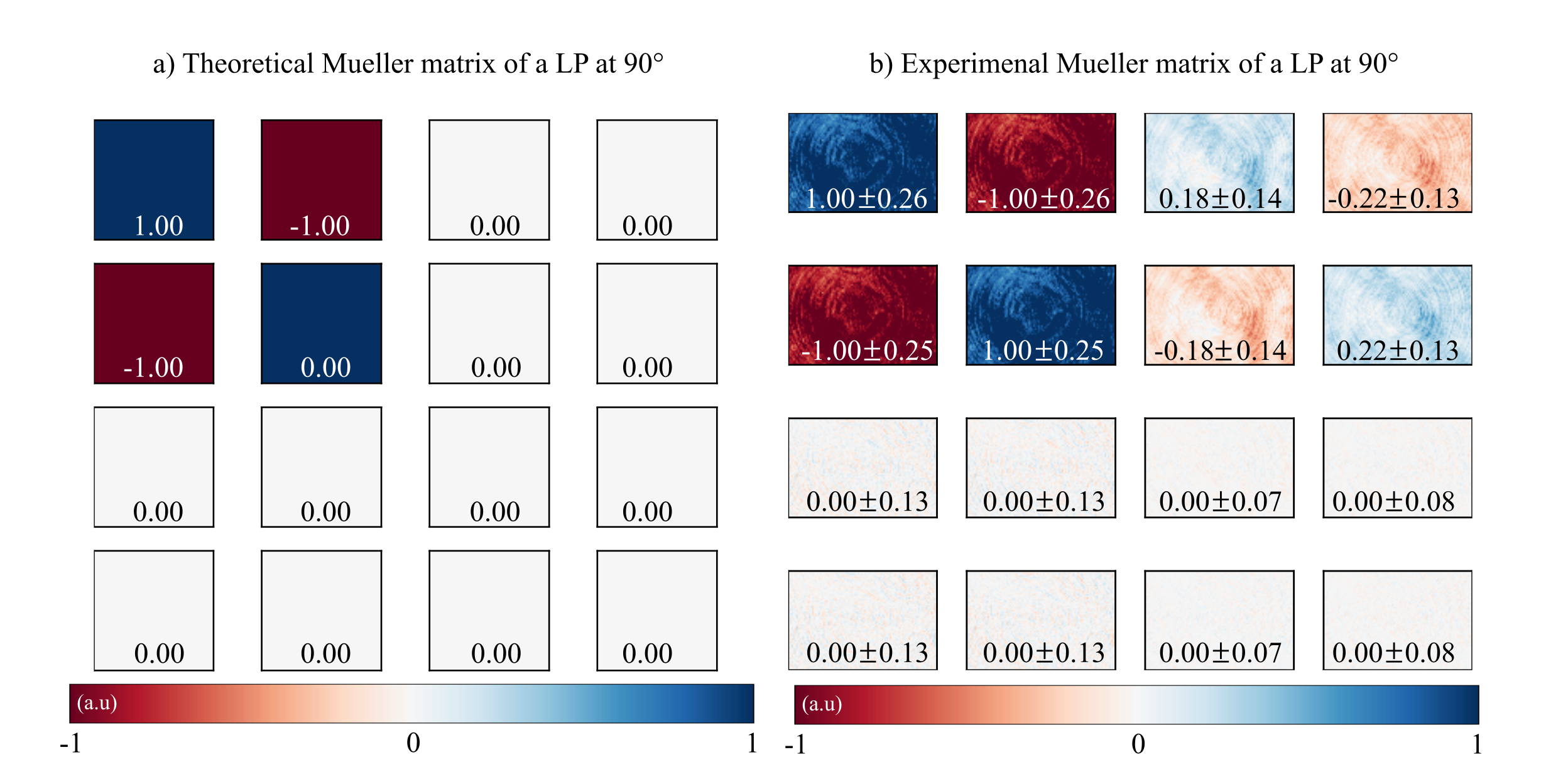
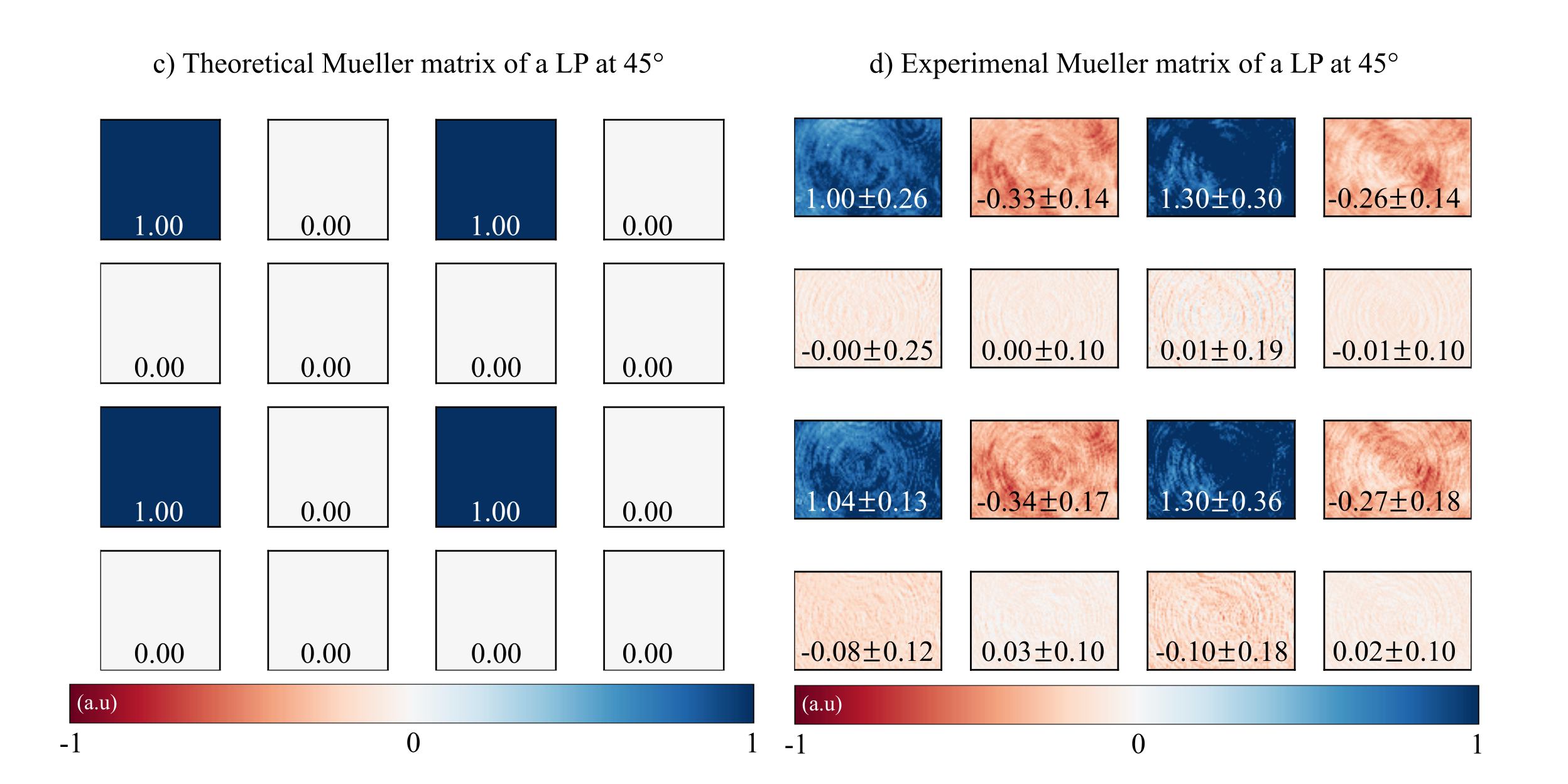
Theoretical values of the Mueller matrices.

$LP_{90^{\circ}}=\begin{bmatrix} 1& -1& 0&0\\ -1& 1 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &0 &0 \end{bmatrix}\: \: \: and\: \: \: LP_{+45^{\circ}}=\begin{bmatrix} 1& 0& 1&0\\ 0& 0 &0 &0 \\ 1 &0 &1 &0 \\ 0 &0 &0 &0 \end{bmatrix}$

The agreement between the experimental and theoretical Mueller matrices is high. The next table compares the experimental and theoretical polarimetric parameters (diattenuation, polarization, depolarization, and angle of polarization) of the linear polarizer for both orientation angles. Again, the degree of correlation between theoretical and experimental results is very high.

	Linear polarizer at 90° Theo.	Linear polarizer at 90° Exp.	Linear polarizer at +45° Theo.	Linear polarizer at +45° Exp.
Diattenuation (a.u)	1	1.01 $\pm$ 0.37	1	1.31 $\pm$ 0.39
Polarization (a.u)	1	1.05 $\pm$ 0.36	1	1.09 $\pm$ 0.24
Depolarization (a.u)	0.42	0.42 $\pm$ 0.21	0.42	0.42 $\pm$ 0.25
Angle (°)	90	90 $\pm$ 4	45	45 $\pm$ 3

Script

The computational method to estimate the Mueller matrix from 36 intensity-based images is implemented in Python and MATLAB.

Samples

We have available the 36 intensity-based experimental images of:

Funding

This project was partially funded by EAFIT University (Medellin, Antioquia, Colombia), and the National Science Foundation (NSF) (grant number 2042563).

Citation

If using this information for publication, please kindly cite the following paper:

S. Obando-Vasquez, A. Doblas, and C. Trujillo, “Apparatus and method to recover the Mueller matrix in bright-field microscopy,” American Journal of Physics 90, 702 (2022). doi: 10/1119/5.0081673.

Support or Contact

Researcher	email	Google Scholar
Sofia Obando-Vasquez	sobandov@eafit.edu.co
Ana Doblas	adoblas@memphis.edu	AnaGoogle
Carlos Trujillo	catrujilla@eafit.edu.co	CarlosGoogle

This Research is a collaboration between Doblas’ and Trujillos’ research lab.